Probability and Stochastic Processes (2nd Edition) Edit edition

This problem has been solved:

…

Let there are two types of pizzas, either regular or Tuscan. Each slice of pizza may have mushrooms or onions.

Let R be an event that the pizza is Regular.

Let T be an event that the pizza is Tuscan.

Let M be an event that the slice of pizza having mushrooms.

Let O be an event that the slice of the pizza having onions.

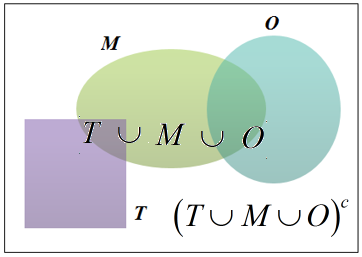
The known Venn diagram is,

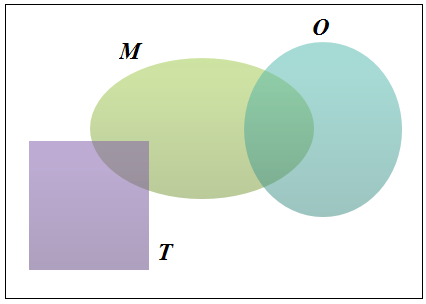
(a)

Determine the events T and M are mutually exclusive or not.

Visually, from the Venn diagram, the events T and M are not mutually exclusive. Because 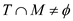. The intersection of two sets T and M is the set of all elements which are contained in both T and M.

(b)

Determine the events R, T and M are collectively exhaustive or not.

Every pizza is either Regular or Tuscan. Here,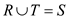so that the pizzas R and T are collectively exhaustive. Therefore, 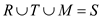is also collectively exhaustive. Because the union of R, T and M is the set of all pizzas that are in either R, or T, or M or in three.

(c)

Are T and O mutually exclusive?

From the Venn diagram, the events T and O are mutually exclusive, if .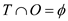

Tuscan pizzas never have onions.

(d)

Gerlanda’s doesn’t make Tuscan pizzas with mushrooms (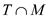) and onions (O). Visually, from the Venn diagram these two events Tuscan pizzas with mushrooms and onions are mutually exclusive.

(e)

Yes. Visually, from the Venn diagram, an event of regular pizzas that have neither mushrooms nor onions is defined as .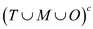

The Venn diagram shows the complimentary event.